Scope:
Leistungsberechnung unter der Voraussetzung periodisch, sinusförmig verlaufender Spannungen und Ströme in Zusammenhang mit kapazitiv und induktiv wirksamen Elementen. Der Fokus liegt auf einphasigen Stromkreisen.
Variierende elektrische Leistung eines Verbrauchers im Gleichstrombetrieb, die sich im längeren zeitlichen Bezug ändert, ist ebensowenig Gegenstand dieser Betrachtungen, wie die im Zuge von Datenübertragung oder Synchronisation erbrachte Leistung.
Problemstellung:
Von Saure in der Wikipedia auf Deutsch – Eigenes Werk des ursprünglichen Hochladers, CC BY-SA 3.0, Link
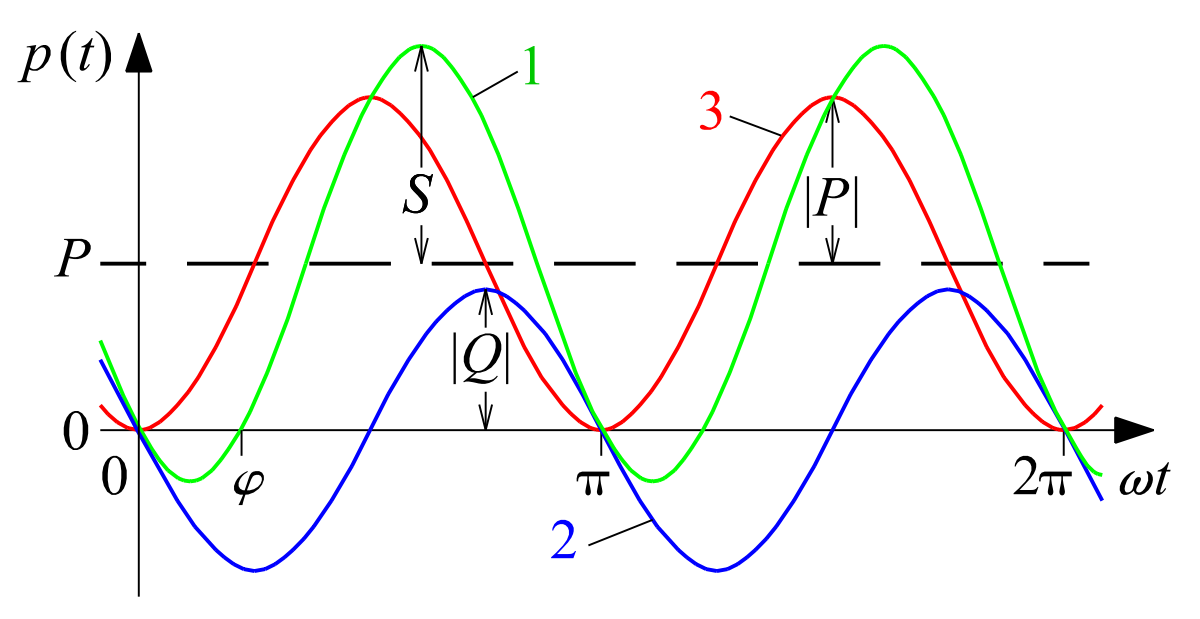
Die obige Abbildung ist dem Artikel über Blindleistung der deutschsprachigen Wikipedia entnommen. Sie stellt den durch Einwirkung einer induktiven Last verursachten Verlauf der Scheinleistung „S“ als grünmarkierten und mit 1 beschrifteten Graphen dar. Durch Addition einer genau bemessenen, kapazitiven Blindleistung „Q“, wie sie der blaumarkierte und mit 2 beschriftete Graph darstellt, entsteht als Summe der Lasten eine summarische Last, die durch eine Leistung „P“ mit dem Verlauf des rotmarkierten und mit 3 beschrifteten Graphen beschrieben wird. Aus der Addition sinusförmiger Verläufe mit gleicher Periodendauer entsteht erneut immer ein sinusförmiger Verlauf unter Beibehalt der Periode aber mit möglicherweise verschobener Phase.
Für die Berechnung der Wirkleistung gilt allgemein:
Die Regeln zur Ermittlung von Leistung gelten auch im Umgang mit Wechselstrom. Periodische, sinusförmig verlaufende Wechselgrößen erlauben vereinfachende Berechnungen zum Beispiel mithilfe der Zeigerdarstellung. Nichtsinusförmige Wechselgrößenverläufe werden durch Induktivitäten und Kapazitäten in einer Weise verzerrt, der möglicherweise zu Verläufen mit einer anderen Periode ganz sicher aber zu Verzerrungen des Signals führen, die nur entfernt an den ursprünglichen Verlauf der Wechselgröße erinnern.
Abbildungen Einschwingvorgang einer Kapazitäten, Rechteckspannung an Kapazität bzw. Induktivität.
Die gezeigten Bauelemente nehmen zeitverzögert Energie auf und geben die gespeicherte Energie zeitverzögert in das System zurück. In das System zurückfließender Strom überlagert (addiert) sich zu dem anderen fließenden Strom.
Nimmt man die Spannung sinusförmig an und legt als Bezugsgröße die Spannung fest wird aus u(t):
Unter der Annahme, das zu untersuchende Bauelement besitzt kapazitive Eigenschaften (z.B. Erdkabel, Koaxialkabel, Kondensatoren, abgeschirmte Kabel, durch eine Platine getrennte Leiterbahnen unterschiedlicher Spannung), eilt der Strom der Spannung voraus. Damit eilt der Strom einen um π/2 voraus. Ihr ebenfalls sinusförmiger Verlauf nimmt damit die Form der Cosinusfunktion an.
Liegt eine induktive Last an, läuft der Strom der Spannung um π/2 hinterher. Es entsteht eine negative Cosinusfunktion.

Von Saure in der Wikipedia auf Deutsch – Eigenes Werk des ursprünglichen Hochladers, CC BY-SA 3.0, Link
Die obige Abbildung ist wieder der deutschen Wikipedia dem Beitrag über Blindleistung entnommen. Sinnvollerweise wäre an die Stelle des „P“ für die Leistung, die in diesem Fall eine Blindleistung ist, ein „Q“ getreten. In jedem Fall ergibt die über eine Periode gemittelte Leistung den Wert 0 Watt.
Durch einen Widerstand fließender Blindstrom führt am Widerstand ebenso zur Erwärmung und damit zu Verlusten wie Wirkstrom. Vor allem aber belastet Blindleistung die Energieerzeuger. Die Regeln
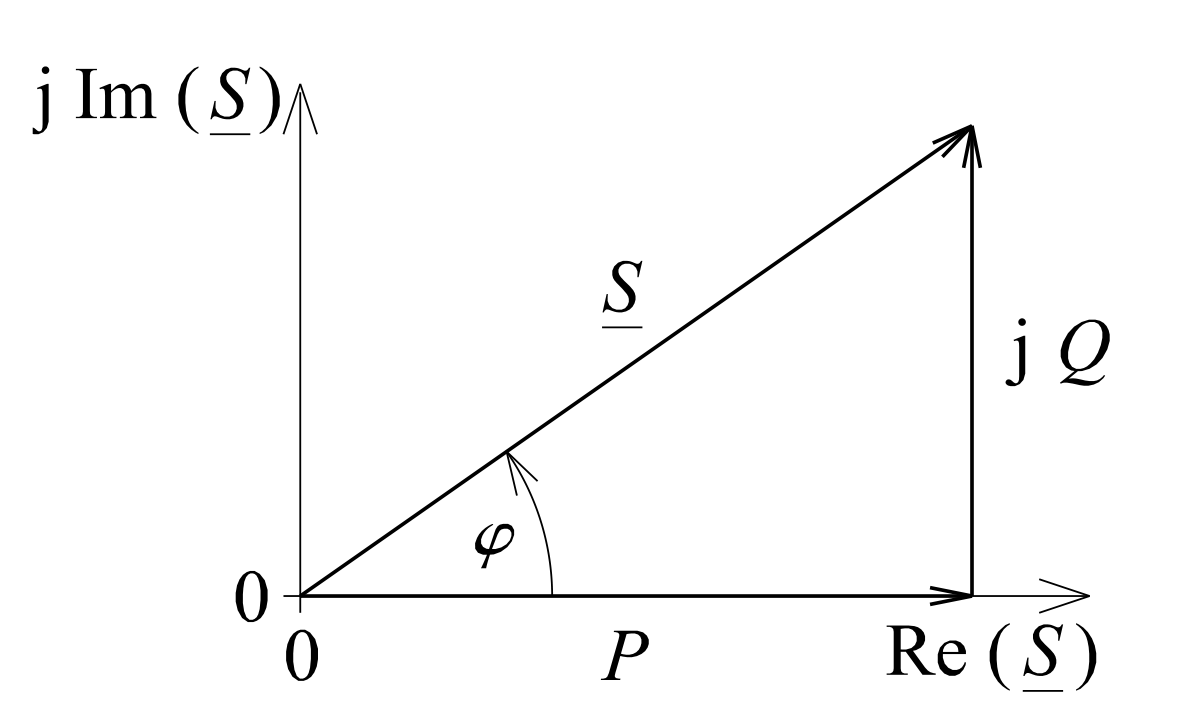
Wechselstromleistung im Zeigerdiagramm
Prinzipiell gilt, das der Widerstand als zeitlich konstante Größe angenommen wird. Dabei ist es gleich, ob es sich um:
R : Den Wirkwiderstand
XL : Den induktiven Blindwiderstand
XC: Den kapazitiven Blindwiderstand
handelt, die gerne zum Scheinwiderstand Z mit dem effektiven Scheinwiderstand als Zeigerlänge und dem Drehwinkel φ zusammengefasst werden.
Zur Ermittlung der Leistungen:
P : Wirkleistung in Watt [W]
Q: Blindleistung in var [var]
S: Scheinleistung in Voltampere [VA]
gelten die gleichen Bedingungen und Bemerkungen wie bei der Bestimmung des Scheinwiderstandes. Im Fall der Leistung, ist aus der Scheinleistung sowohl die Wirk- als auch die Blindleistung mittels trigonometrischer Funktionen zu bestimmen.
Von Saure in der Wikipedia auf Deutsch – Eigenes Werk des ursprünglichen Hochladers, CC BY-SA 3.0, Link
Bei der Bestimmung von Gleichstromwiderständen aus der Messung vom durch den Widerstand fließenden Strom und der am Widerstand abfallenden Spannung ergeben sich abhängig vom Messaufbau ein Stromfehler oder ein Spannungsfehler, da jedes Messgerät selbst einen Widerstand besitzt. In der Leistungsmessung verbraucht auch der Leistungsmesser Leistung und je nach Implementation kommt es ebenfalls zu einer Fehlmessung, dessen Folgen entweder der Verbraucher oder der Erzeuger tragen.
Die folgenden Formulierungen sowie Abbildungen entstammen dem Artikel über Wirkleistung der deutschen Wikipedia:
Keine der Schaltungen erfasst aber die Erzeuger- oder Verbraucher-Wirkleistung, sondern gemessen wird
- in der oberen Schaltung Erzeuger-Spannung mal Verbraucher-Strom,
- in der unteren Schaltung Verbraucher-Spannung mal Erzeuger-Strom.
In der bevorzugt verwendeten oberen Schaltung werden die Kosten des Energie-Verbrauchs des Messgerätes getragen
-
- soweit vom Spannungspfad herrührend durch den Erzeuger,
- soweit vom Strompfad herrührend durch den Verbraucher.

Von Saure 18:27, 30. Apr. 2009 (CEST) – selber konvertiert, CC BY-SA 3.0, Link
Stand: 18.02.2018 Revision 0.0.1
