Die Trigonometrie beschreibt mathematische und geometrische Zusammenhänge in Dreiecken. Umgang mit und die Berechnung von Elementen in Dreiecken ist Teil von Aufgaben in der Programmierung von Grafiken (z.B. in Spielen), der Physik (Optik, Bauingenieurswesen mit z.B. Statik) aber auch Elektrotechnik (Energietechnik, elektrische Maschinen) und Maschinenbau.
Eine Grunderkenntnis von Trigonometrie:Die Summe aller Winkel im Dreieck beträgt 180° (Grad).
Die Aussage: Dreiecke sind einander ähnlich, wenn ihre Winkel gleich sind, ist Grundlage einige Vergrößerungs(Zoom)funktionen in Computerspielen. Ebenso allerdings wird sie bei der Skalierung von konstruktiven (z.B. Elektrotechnik und Statik) Überlegungen eingesetzt.
Wichtige Sonderfälle sind das rechtwinklige sowie das gleichschenklige Dreieck. Ein Dreieck bezeichnet man als rechtwinklig, wenn einer der (Innen-)winkel 90° beträgt.
In einem rechtwinkligen Dreieck gibt es eine längste Seite. Längste Seiten im Dreieck liegen immer dem größten Innenwinkel gegenüber. Die längste Seite im rechtwinkligen Dreieck heißt Hypotenuse. Die beiden kürzeren Seiten im rechtwinkligen Dreieck heißen Katheten.
Ist die Lage und Länge der Hypotenuse bekannt, dann liegt der gegenüberliegende Eckpunkt des Dreiecks auf einem Halbkreis, dessen Mittelpunkt in der Mitte der Hypotenuse liegt. Dieser Kreis heißt Thaleskreis. Im Bereich elektrischer Antriebe und Maschinen gewinnt dieser Kreis seine Bedeutung in der Elektrotechnik und wird dort behandelt.
 Von MartinThoma – Eigenes Werk, CC0, Link
Von MartinThoma – Eigenes Werk, CC0, Link
Für rechtwinklige Dreiecke gilt der Satz des Pythagoras: Die Summe der Quadrate über den beiden Katheten entspricht dem Quadrat über der Hypotenuse.
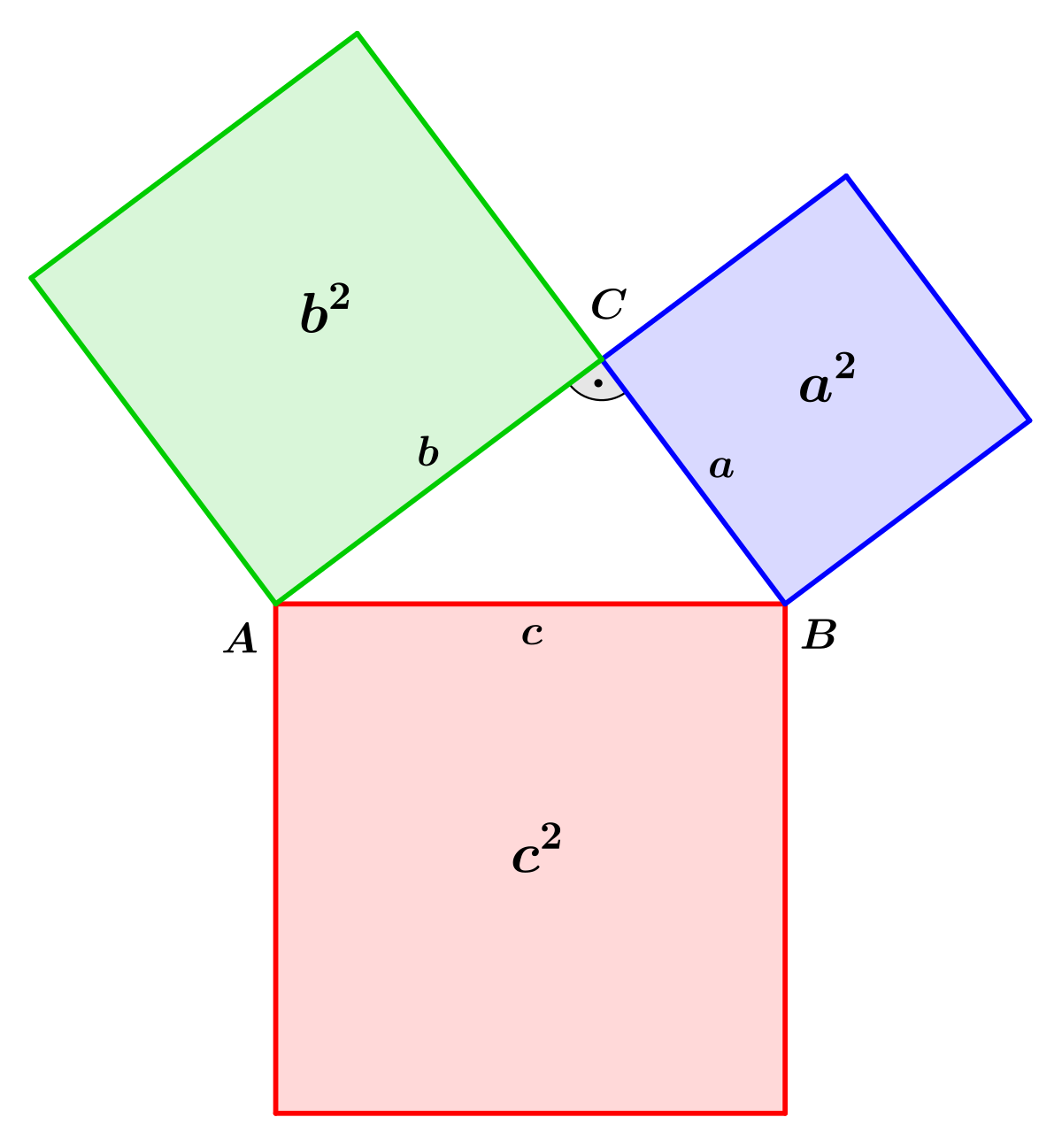
Von Petrus3743 – Eigenes Werk, CC-BY-SA 4.0, Link
Ein Dreieck gilt dann als gleichschenklig, wenn zwei seiner Seiten die gleiche Länge besitzen. Derartige Dreiecke zeigen ihren Bedeutung bei der Konstruktion visueller Effekte zum Beispiel in Flugsimulationsspielen. Sind in einem Spezialfall alle 3 Seiten eines Dreiecks von gleicher Länge, nennt man das Dreieck gleichseitig. Gleichseitige Dreiecke sind immer auch gleichschenklig. Im gleichseitigen Dreieck alle die eingeschlossenen Winkel jeweils gleich groß. Der Winkel beträgt 60°.
Im gleichschenkligen Dreieck bezeichnet man die Seite, deren Länge sich von der Länge der beiden anderen Seiten unterscheidet als Basis. Die Winkel die die gleichlangen Schenkel mit der Basis bilden sind gleich groß. Sie heißen Basiswinkel.
 Von MartinThoma – Eigenes Werk, CC BY 3.0, Link
Von MartinThoma – Eigenes Werk, CC BY 3.0, Link
Auf der violett gezeichneten Mittelsenkrechten der Basis liegen drei für die Anwendung von Dreiecken wichtige Punkte.
Der zuoberst und blau eingezeichnete Punkt beschreibt den Umkreismittelpunkt. Er entsteht als Schnittpunkt der Mittelsenkrechten der drei Seiten des Dreiecks. Ein dreieckiges Objekt, das sich um diesen Punkt dreht, benötigt den kleinsten Durchmesser für die Drehung.
Der mittlere und rot eingezeichnete Punkt beschreibt den Schwerpunkt eine Dreiecks. Er entsteht als Schnittpunkt der Verbindungslinien zwischen den Eckpunkten eines Dreiecks und den Fußpunkten der Mittelsenkrechten (Seitenhalbierende). Das menschliche Auge zeigt sich sehr sensibel für Verschiebungen des Schwerpunkts. Das optische Gleichgewicht erscheint „gestört“.
Der unterste und grün eingezeichnete Punkt beschreibt den Innenkreismittelpunkt. Er entsteht als Schnittpunkt von Graden die in jeweils in einer Ecke des Dreiecks beginnen und den eingeschlossenen Winkel halbieren (Seitenhalbierende). Der Mittelpunkt des größten, innerhalb des Dreiecks liegenden konstruierbaren Kreises liegt an diesem Punkt.
Formeln zur Berechnung dieser Punkte finden sich tabellarisch im Beitrag der Wikipedia zum gleichschenkligen Dreieck. Eine gute Zusammenfassung zur Dreiecksberechnung für die Mittelstufe findet sich in dem Aufsatz Schulmathematik: Trigonometrie der Wikibooks.
Meist sind Fragestellungen in Bezug auf Längen und Winkel in allgemeinen Dreiecken über den Umweg der Bildung rechtwinkliger Dreiecke lösbar.
Zitat zum Sinus- und Cosinussatz aus dem Wikibook „Schulmathematik: Trigonometrie„:
Der Sinus, Kosinus und Tangens kann nur in einem rechtwinkligen Dreieck verwendet werden. Mithilfe von Sinus- und Kosinussatz kann man jedes Dreieck berechnen solange genügend Werte vorhanden sind, denn jedes Dreieck kann in zwei kleine rechtwinkelige Dreiecke zerlegt werden.
Mit der Dreiecksberechnung erhalten also auch die Funktionen Sinus, Cosinus und Tangens Einzug. Diese Funktionen beziehen sich stets auf die Verhältnisse im rechtwinkligen Dreieck. Da alle Dreiecke durch Unterteilung in rechtwinklige Dreiecke zerlegt werden können (s.o.), reicht an dieser Stelle die explizite Behandlung der Verhältnisse im rechtwinkligen Dreieck. Zur weiteren Vereinfachung wird die Länge der Hypotenuse zu 1 angenommen. Ein Dreieck ist festgelegt durch:
- die Länge einer Seite und zwei Winkel
- die Länge zweier Seiten und ein Winkel
- die Länge aller drei Seiten.
Unter der Voraussetzung, das zu betrachtende Dreieck ist rechtwinklig und die Hypotenuse ist von der Länge 1, ergeben sich mögliche Dreiecke, die auf einem Kreis mit dem Radius 1 liegen (Einheitskreis).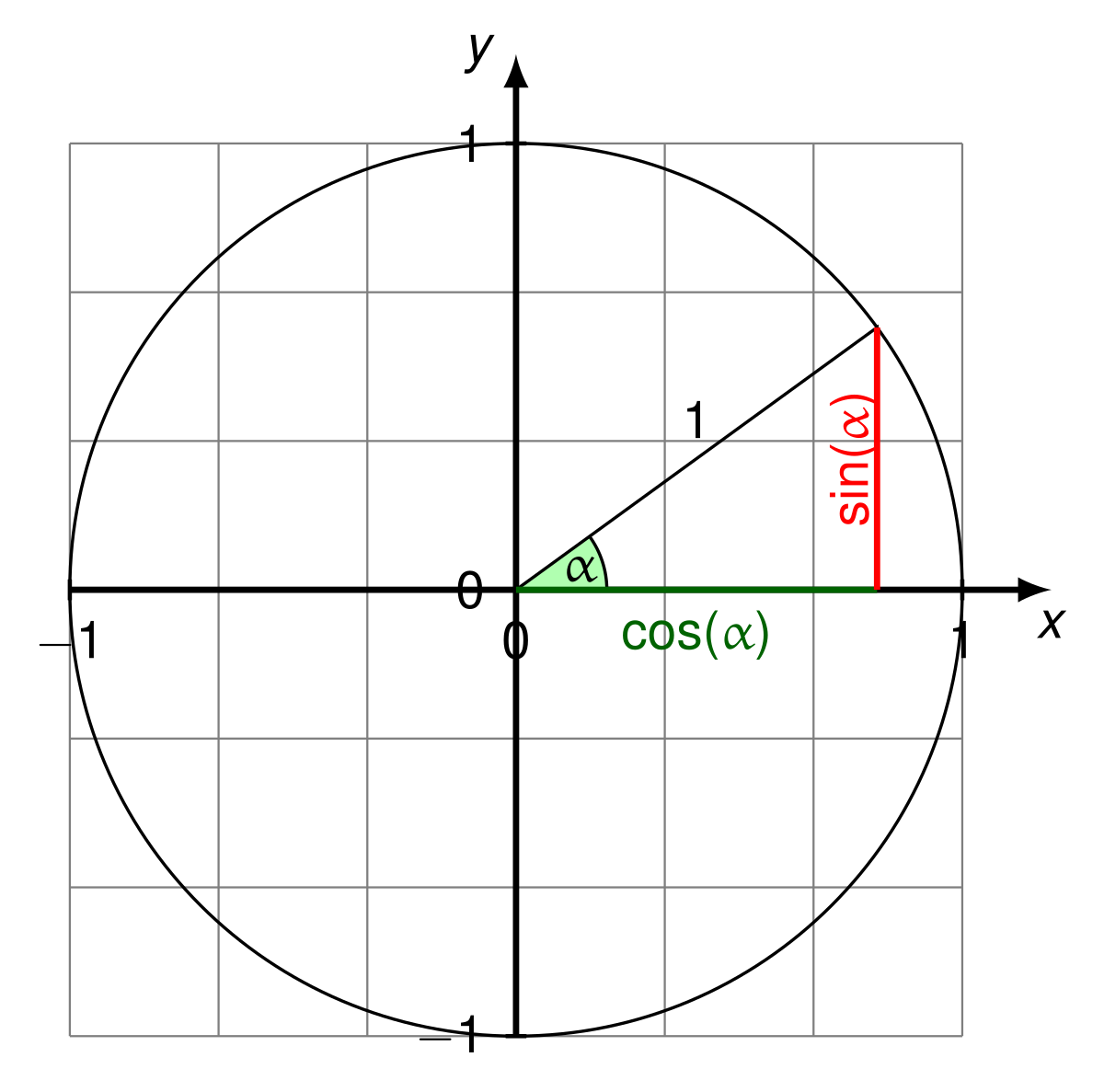 Von MartinThoma – Eigenes Werk, CC0, Link
Von MartinThoma – Eigenes Werk, CC0, Link
Der Sinus des Winkels α ergibt sich aus dem Verhältnis von Gegenkathete zu Hypotenuse. Besondere Stützstellen ergeben sich mit α = 0, denn dann beträgt die Länge der Gegenkathete und damit der sin(α) Null. Mit α = 90° ergibt sich sin(α) zu 1 und mit α = 180° ergibt sich sin(α) wieder zu 0. Ist α = 270° wird sin(α) zu -1. Der Verlauf von sin(α) lässt sich graphisch als vom Drehwinkel abhängige Größe auftragen. Dem Drehwinkel entsprechend wird an der Stelle des Drehwinkels der Umfang des Einheitskreises als Maß für die fortschreitende Zunahme des Winkels aufgetragen. Der Umfang den Einheitskreises beträgt 2π . Dem Drehwinkel α von 90° entsprecht ein Umfang von π/2, einem Drehwinkel α von 180° entspricht eine Umfang von π, bei 270° sind es 3 π/2 und bei 360° 2 π . Damit ergibt sich das folgende Bild:

Von Geek3 – Eigenes Werk, GFDL, Link
Der Cosinus des Winkels α ergibt sich aus dem Verhältnis von Ankathete zu Hypotenuse. Besondere Stützstellen ergeben sich mit α = 0, denn dann beträgt die Länge der Ankathete und damit der cos(α) 1. Mit α = 90° ergibt sich cos(α) zu 0 und mit α = 180° ergibt sich cos(α) zu -1. Ist α = 270° wird cos(α) zu 0. Auch der Verlauf von cos(α) lässt sich graphisch als vom Drehwinkel abhängige Größe auftragen. Dem Drehwinkel entsprechend wird an der Stelle des Drehwinkels der Umfang des Einheitskreises als Maß für die fortschreitende Zunahme des Winkels aufgetragen. Der Umfang den Einheitskreises beträgt 2π . Dem Drehwinkel α von 90° entsprecht ein Umfang von π/2, einem Drehwinkel α von 180° entspricht eine Umfang von π, bei 270° sind es 3 π/2 und bei 360° 2 π . Damit ergibt sich das folgende Bild:

Von Geek3 – Eigenes Werk, GFDL, Link
Der Tangens des Winkels α ergibt sich aus dem Verhältnis von Gegenkathete zu Ankathete. Da der Sinus der Quotient aus Gegenkathete und Hypotenuse und der Cosinus der Quotient aus Ankathete und Hypotenuse ist, kann der Tangens auch als Quotient aus Sinus und Cosinus aufgefasst werden. Der Dividend „Hypotenuse“ entfällt dann durch Kürzen. Damit ergibt sich ein im Vergleich zu Sinus und Cosinus gänzlich unterschiedliches Bild, denn immer dann wenn der Cosinus den Wert 0 besitzt, entstehen Punkte im Kurvenverlauf, die – abhängig vom bei gleichem Vorzeichen von Sinus und Cosinus – gegen den positiven Unendlichkeitswert beziehungsweise – bei ungleichen Vorzeichen von Sinus und Cosinus – gegen den negativen Unendlichkeitswert streben. Damit ist der Tangens an diesen Punkten nicht definiert. Ist die Sinusfunktion 0 wird auch der Tangens 0. Damit ergibt sich das folgende Bild:

Von Geek3 – Eigenes Werk, GFDL, Link
Ist die Größe des Winkels α gesucht, weil zum Beispiel die Länge der beiden Katheten bekannt sind, führt die jeweilige Arkus-Umkehrfunktion zum Ziel. Es gibt unterschiedliche Schreibweisen (zum Beispiel auf dem Taschenrechner) arcussinus = arcsin = asin. Entsprechend für den Arkuskosinus arcuscosinus = arccos = acos. Auch gesehen wurde schon eine Bedienung als sin-1() für die inverse Berechnung des Sinus. Das Nämliche gilt für die Tangensfunktion. Da die trigonometrischen Funktionen Sinus, Cosinus und Tangens, Cotangens periodische Funktionen sind, ist der gültige Wertebereich einzuschränken.
Die Verwendung der trigonometrischen Funktionen erlaubt eine Umwandlung Angaben, die im Polarkoordinatensystem erfolgen in Angaben ein karthesischen Koordinatensystems. Der oben verangehend verlinkte Wikipedia-Beitrag über das Polarkoordinatensystem erklärt das entsprechende Vorgehen.
Die Abbildungen wurden der deutschen Wikipedia entnommen. (Stand 0.0.3 vom 13.1.18)
