Begriffe zur Beschreibung des zeitlichen Verlaufs
Klassische Wechelgrößen sind physikalische Größen wie Strom, Spannung in der Elektrotechnik und zum Beispiel Schalldruck in der Akustik. Typischerweise besitzen sie einen geringen oder kleinen Gleichanteil. Periodizität, also regelmäßige Änderungen bestimmen ihren zeitlichen Verlauf.
Auch wenn viele physikalischen Wechselgrößen einen sinusförmigen, zeitlichen Verlauf zeigen, sind Abweichungen von davon nicht selten. Die folgende Abbildung zeigt Beispiele für einige typische Formen.

Von Image:Waveforms.svg, CC BY-SA 3.0, Link
Typische allgemeine Eigenschaften von Wechselgrößen sind:
- Periodizität (Periodendauer),
- Amplitude,
- Form.
In der Elektrotechnik können weitere Größen zur Beschreibung wie Effektivwert, Tastverhältnis/Tastgrad und Pulsweite hinzutreten.
Periodizität
Unter der Periodizität einer Wechselgröße versteht man das Wiederkehren eines bestimmten Verlaufs oder Musters in festen Zeitabständen. Die Zeit vom Beginn einer Periode bis zum Beginn der nächsten Periode bezeichnet man als Periodendauer. Die Periodendauer wird in Sekunden bzw. Vielfachen oder Bruchteilen von Sekunden gemessen. Den Kehrwert der Periodendauer bezeichnet man als Frequenz.
Beispiel: Ergeben sich 100 vollständige Perioden innerhalb einer Sekunde, beträgt die Periodendauer 1/100 Sekunden oder 10 ms. Wird eine Darstellung als Frequenz benötigt, ergibt der Kehrwert von 1/100 genau 100. Frequenz wird der Einheit Hz [sprich: Hertz] angegeben. 1 Hz entspricht demnach 1/s.
Amplitude
Die Amplitude gibt bei einer symmetrischen Wechselgröße den innerhalb einer Periode Maximalwert der Wechselgröße an. Die Variable der betrachteten Größe erhält typischerweise ein „Dach“. So drückt das „^“ bei einer zeitlich veränderlichen Größe wie der Spannung u(t) verwendete û den Spitzenwert aus. Bei einem rechteckigen Verlauf der Wechselgröße „Spannung“ bleibt die Amplitudenspannung einige Zeit bestehen. Bei anderen Verlaufsformen kann der Spitzenwert ein beliebig kurzer Augenblickswert sein.
Typische Kenngrößen eines sinusförmigen Spannungsverlaufs

Von Saure – Eigenes Werk, Gemeinfrei, Link
1 = Amplitude = û
2 = Spitze-Tal-Wert oder Spitze-Spitze-Wert = USS
3 = Effektivwert = Ueff
4 = Periodendauer = T
Periodisch verlaufende Wechselgrößen lassen sich oft zumindest theoretisch auf eine Überlagerung von Vielfachen der sinusförmigen Wechselgröße beschreiben, wie das Beispiel eines Rechtecksignals zeigt.
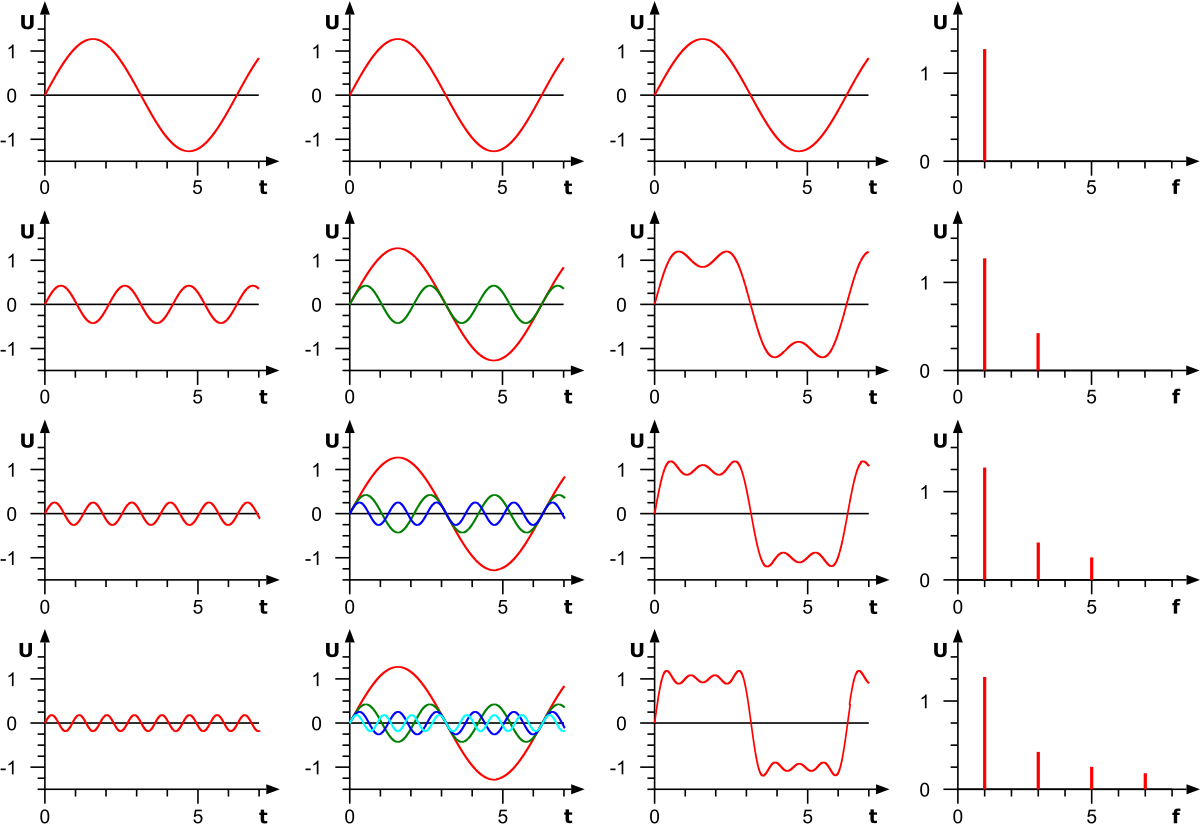
Von René Schwarz – Eigenes Werk, SVG Version of File:Fouriersynthese.png, CC BY-SA 3.0, Link
Hier werden ungrade ganzzahlige Vielfache einer Grundfrequenz phasengleich überlagert. Bekannt ist diese Art der Überlagerung als Fouriersynthese. Umgekehrt lassen sich periodische Signalverläufe oft auch entsprechend diesem Verfahren zerlegen (Fourierzerlegung). Die jeweils rechte, äußere Spalte der Grafiken stellt diese Zerlegung dar. Auch die Sägezahnschwingung lässt sich auf diese Weise als Überlagerung mehrerer sinusförmiger Schwingungen beschreiben.
Damit erklärt sich, warum physikalische Zusammenhänge, die für sinusformige Verläufe von Wechselgrößen gelten zumindest in Näherung auch für andere periodisch verlaufende Wechselgrößen gelten.
Da sinusförmige Wechselgrößen einander überlagern und zu anderen Formen von Verläufen führen können, liegt es nahe, dass einer periodischen Wechselgröße auch ein Gleichanteil überlagert werden kann. Damit verliert die Summe dieser Komponenten zwar den Anspruch, eine „klassische“ Wechselgröße zu sein, die Aussagen zu ihrem Verhalten in technischen Anlagen wie beispielsweise eine mögliche frequenzabhängige Signaldämpfung, bleibt jedoch erhalten.
