Addition von Wechselgrößen mit unterschiedlicher Phasenlage [Stand 0.0.1]
Knotenregel (1. Kirchhoffsche Regel; 1. Kirchhoffsches Gesetz; Knotenpunktregel …)
In einem Knotenpunkt eines elektrischen Netzwerks addieren sich alle Ströme zu Null. Nach einer anderen Formulierung entspricht in einem Knotenpunkt die Summe der zufließenden Ströme der Summe der abfließenden Ströme.
Voraussetzung der Regel ist:
- Es findet keine energetische/chemische Umsetzung im Knoten statt.
- Es gibt keinen lokalen Speicher, der zum Beispiel für eine Verzögerung sorgt.
Trivial formuliert: Alles was reingeht muss auch sofort wieder herauskommen. Es gibt also keinen „Puffer“ für Ladung.
Unter diesen Voraussetzungen gilt die Regel sowohl für Gleichstrom- als Wechselstromknotenpunkte in einem Netzwerk.

Von Philnate in der Wikipedia auf Deutsch – Datei:Stromknoten.png Übertragen aus de.wikipedia nach Commons durch Wdwd mithilfe des CommonsHelper., Gemeinfrei, Link
Abbildung eines Stromknotens. Entnommen aus: de.wikipedia.org/wiki/Kirchhoffsche_Regeln
Interessant wird die Knotenregel mit Blick auf sich addierende Wechselgrößen mit unterschiedlicher Phasenlage (immer unter der Voraussetzung, dass sie eine identische Periode besitzen und ihr Verlauf sinusförmig ist).
Komplexe Wechselstromwiderstände = Impedanzen = Scheinwiderstände beeinflussen die Phasenlage von Wechselgrößen.
Ideale Spulen und Kondensatoren besitzen keinen ohmschen Widerstand. Ihr Widerstand gegen sinusförmig wechselndem Strom oder Spannung äußert sich demnach in einem Blindwiderstand. Auch an komplexen Wechselstromwiderständen wird Leistung umgesetzt. Die an dem Blindwiderstand der idealen Spule und idealen Kondensator umgesetzte Leistung ist demzufolge eine Blindleistung. Reale Bauelemente von Spule und Kondensator besitzen immer ebenso wie die die verbindenden Leitungen einen – wenn auch geringen – ohmschen Widerstand, der in realen, technischen Aufbauten nicht vernachlässigt werden darf. Meist lässt sich der ohmsche Anteil aus Bauelement und Leitung zu einem Gesamtwiderstand zusammenfassen, sodass in der Regel ein aus Blindwiderstand und ohmschen Widerstand zusammengesetzter komplexer Widerstand entsteht an dem entsprechend seinen Anteilen von ohmschem Widerstand Wirkleistung und Blindwiderstand Blindleistung umgesetzt wird. Wirkleistung und Blindleistung addieren sich zur Scheinleistung. Sowohl eine Berechnung über die trigonometrischen Größen als auch eine anschaulichere vereinfachende Darstellung und Rechnung mit Zeigern ist möglich.
Der Entstehung an den prinzipiell unterschiedlichen Bauelementen Kondensator und Spule entsprechend spricht man auch von kapazitiver Blindleistung und induktiver Blindleistung.
Spule und Kondensator beeinflussen die Phasenlage von Wechselgrößen in entgegengesetzter Richtung. Weiterhin ist den
Formeln zur Berechnung der Wechselstromwiderstände ist zu entnehmen:
- Der Wechselstromwiderstand einer Kapazität (z.B. eines Kondensators) nimmt mit steigender Frequenz hyperbolisch ab.
- Der Wechselstromwiderstand einer Induktivität (Spule) wächst proportional zur Frequenz.
Den Zusammenhang zwischen Frequenz und Wechselstromwiderstand geben die folgenden Darstellungen anschaulich wider.
 Von Zátonyi Sándor, (ifj.) Fizped – Eigenes Werk, CC BY 3.0, Link
Von Zátonyi Sándor, (ifj.) Fizped – Eigenes Werk, CC BY 3.0, Link
Scheinwiderstand eines Kondensators bei C = 1µF aufgetragen gegen die Frequenz
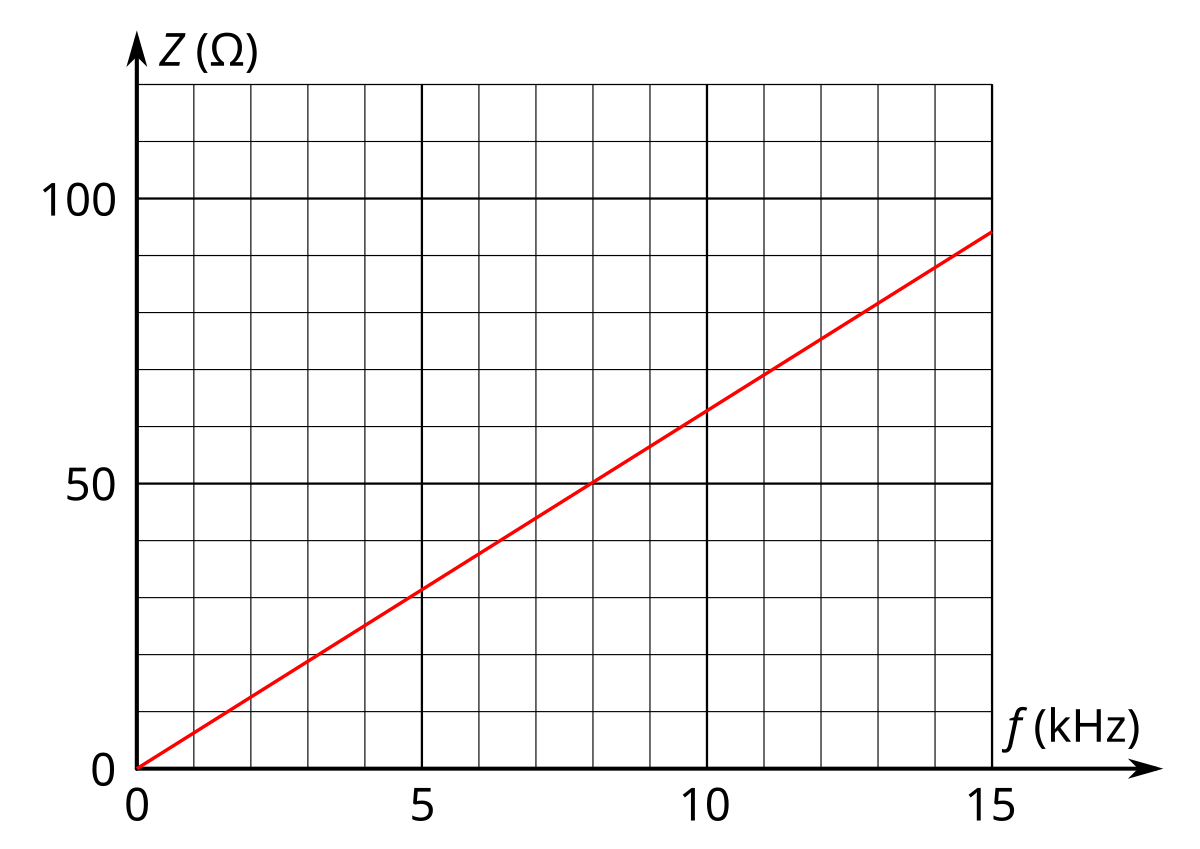 Von Zátonyi Sándor, (ifj.) Fizped – Eigenes Werk, CC BY 3.0, Link
Von Zátonyi Sándor, (ifj.) Fizped – Eigenes Werk, CC BY 3.0, Link
Scheinwiderstand einer Spule bei L = 1 mH aufgetragen gegen die Frequenz
Da ein rein ohmscher Widerstand frequenzunabhängig ist, erübrigt sich eine Darstellung einer Frequenzabhängigkeit. Ein zur Frequenzachse parallele Linie wäre darzustellen.
Für Darstellung von Spannung, Strom und Leistung im Zeigerdiagramm gelten die Vereinbarungen:
- Ausgangsposition eines Zeiger (0° Phasenwinkel φ = 0°). Der Zeiger, dargestellt als im Ursprung beginnender Pfeil liegt horizontal und zeigt nach rechts.
- Die Länge des Zeiger gibt den Effektivwert an.
- Der Phasenwinkel φ > 0 ergibt sich als Steigung in einem linksdrehenden, also gegen den Uhrzeiger drehenden Sinn.
Eine Kapazität (z.B. Kondensator) bewirkt im Wechselstromkreis einen gegenüber der Spannung um einen Phasenwinkel von +90° vorauslaufenden Strom. Der Stromzeiger zeigt gegenüber dem Spannungszeiger rechtwinklig nach oben.
Eine Induktivität (z.B. Spule) bewirkt im Wechselstromkreis einen gegenüber der Spannung um einen Phasenwinkel von 90° nacheilenden Strom (φ = -90°). Der Stromzeiger zeigt gegenüber dem Spannungszeiger rechtwinklig nach unten.
Die beiden Einflüsse lassen sich auch im Bogenmaß im Fall des Kondensators mit +π/2 und im Fall der Spule -π/2 ausdrücken.
Eine Veranschaulichung des Problems gibt die deutschsprachige Wikipedia unter dem Kapitel Blindleistung. https://de.wikipedia.org/wiki/Blindleistung
In aller bayrischen Munde ist die Erdverkabelung der von der Nordsee kommenden Hochspannungsleitung auf bayrischem Grund. Dieser Wunsch bringt enorme Extrakosten im Betrieb mit sich, wie die Wikipedianer an einem Beispiel eines Erdkabels in Berlin zeigen.
Zitat: „Erdkabel stellen aufgrund des geringen Abstandes der Adern zueinander bei gegebener Länge eine große kapazitive Last dar. Die rund 11,5 km lange 380-kV-Transversale Berlin hat eine Kapazität von 2,2 μF. Um diese mit 50 Hz umzuladen, muss Blindstrom von 160 A aufgebracht werden, das entspricht einer Blindleistung von 110 Mvar.“
Auch in der Tontechnik spielt die Impedanz eine große Rolle, denn hier werden mehr oder weniger sinusförmige Signale mit Frequenzen zwischen 50 Hz und 20 kHz übertragen. Mit zunehmender Kabellänge wächst die Dämpfung insbesondere in den hohen Frequenzen (Obertönen), wie die obige Abbildung zeigt. Ein Online-Rechner zu diesem Thema findet sich hier.
Die Zellbiologie nutzt die Änderung von Impedanzen, wie sie durch auf Goldoberfläche wachsenden Zellen verursacht wird, um Änderungen von Zellformen und Zellzahl in Zytotoxizitätstests zu verfolgen. Zellen verhalten sich aufgrund ihrer isolierenden Zellmembran wie elektrische Kapazitäten. Das Verfahren wird Electric Cell-Substrate Impedance Sensing genannt (und hier).
Ohne das Beispiel des Erdkabels oder der Tontechnik im Detail nachrechnen zu wollen, denn die Dimensionierungen der Kabel, Materialangaben etc. sind nicht gegeben, lohnt sich der Gedanke an kapazitive und induktive Kopplungen nicht nur bei der Verlegung langer Kabel sondern auch auf Platinen, in Rechnerräumen und in der Hausinstallation. Es ist nie gleichgültig wo, wie und durch welches Material getrennt Leitungen installiert werden. Es sind die einschlägigen Normen zu berücksichtigen.
Addition gleichfrequenter Wechselströme mit unterschiedlicher Phasenlage
Abbildung Knotenpunkt mit 2 zufließenden Strömen und 1 abfließendem Strom
Es gilt nach der Knotenregel:
I1 + I2 + (-I3) = 0
I3 geht mit negativem Vorzeichen in die Summe ein, weil angenommen wird (entsprechend der Zeichnung), dass es sich um einen abfließenden Strom handelt. Es kann also auch geschrieben werden:
I1 + I2 = I3
Die Aussage gilt unabhängig davon, ob es sich bei den Strömen um Wechselströme oder Gleichströme handelt.
Es soll gelten i1(t) und i2(t) sind Wechselströme und i2(t) eilt dem Strom i1(t) um 90° nach. Für die Amplituden seien 2 A respektive 3 A anzunehmen. Wie stellt sich unter diesen Voraussetzungen der Summenstrom i3(t) dar?
Die Addition sinusförmiger Wechselgrößen mit gleicher Frequenz führt zu einer sinusförmiger Wechselgröße mit der gleichen Frequenz.
Die Amplituden und Effektivwerte können nicht einfach addiert werden, wenn die Phasen nicht synchron verlaufen.
Es lässt sich einerseits formulieren:
und für I2
Damit wird I3 zu:
Durch die Verwendung von Zeigern lässt sich die Aufgabe relativ einfach lösen.
Der Stromzeiger von I2 steht im 90°-Winkel zu I1. Sein Winkel ist positiv also gegen den Uhrzeiger im Verhältnis zu I1 gedreht. Zur Addition können die Zeiger aneinander gesetzt werden.
Abbildung Zeiger von I1 horizontal von links nach rechts und an seiner Spitze beginnt der Zeiger von I2, welcher senkrecht nach oben verläuft.
Die Zeigerlänge entspricht den Effektivwerten. Also:
Durch diese Addition der Stromzeiger entsteht ein Summenstromzeiger I3, dessen Ursprung der Beginn des Zeiger von I1 und dessen Ende die Spitze von I2 markiert. Die Länge des Zeigers von I3 lässt sich über die pythagoreische Summe ermitteln:
Der nach oben gerichtete Winkel errechnet sich aus dem Verhältnis der Ströme I2 zu I1. Da diese beiden Ströme rechtwinklig zueinander stehen, bilden sie die Katheten ein Steigungsdreieck. Der Steigungswinkel φ zwischen I1 und I3 ergibt sich aus dem Arcustangens von I2 zu I1.
Zur Umwandlung in die Sinusfunktion ist zunächst der Effektivwert des Stromes I3 in seinen Amplitudenwert umzuwandeln.
![]() Für den Aufbau der Sinusfunktion ist der Winkel φ des Zeigers I3 noch als Vielfaches von π auszudrücken.
Für den Aufbau der Sinusfunktion ist der Winkel φ des Zeigers I3 noch als Vielfaches von π auszudrücken.![]() I3 läuft I1 also um ungefähr π/3 nach.
I3 läuft I1 also um ungefähr π/3 nach.
Addition komplexer Widerstände
Wie oben angedeutet, besitzen reale Kapazitäten (z.B. Kondensator, Kabel) und Induktivitäten (z.B. Spule, Transformator, Elektromotor) immer einen zumindest geringen ohmschen Widerstand zusätzlich zu ihrem Scheinwiderstand. Diese Kombination lässt komplexe Widerstände aus Wirkwiderstand und Blindwiderstand entstehen.
Wie obige Tabelle ausweist, zeigt der Imaginärteil (also der Blindwiderstand) von Induktivitäten (+) und Kapazitäten (-) in entgegengesetzte Richtungen. Im Gegensatz zu den Verhältnissen bei den Wechselgrößen Strom und Spannung bleiben Wirkwiderstand und Blindwiderstand konstant. Es sind also eingangs keine Effektivwerte zu ermitteln.
Abbildung 15 Ω Wirkwiderstand und 100 µF Kondensator in Reihenschaltung als Ersatzschaltbild Wechselspannung mit 50Hz. (analog zum Wikipediabeispiel)
Zunächst ist der kapazitive Blindwiderstand zu ermitteln mit:
Wobei es sich um einen Blindanteil handelt, der in -90°Richtung zeigt. Der komplexe Wechselstromwiderstand ergibt sich damit zu 15 Ohm Wirkwiderstand und -31,83 Ohm Blindwiderstand.
Der aus Wirkwiderstand und Blindwiderstand bestehende Scheinwiderstand errechnet sich aus der pythagoreischen Summe der erstgenannten Widerstände zu:
Dies entspricht der Länge des Zeigers. Wirkwiderstand und Blindwiderstand bilden die Katheten eines rechtwinkligen Dreiecks. Dessen Hypotenuse der Länge des Scheinwiderstands entspricht. Das Verhältnis von Gegenkathete (Blindwiderstand) zur Ankathete (Wirkwiderstand) ergibt den Tangens des Steigungswinkels, der hier der Phasenverschiebungswinkel ist.
Damit ergibt sich der Zeiger des komplexen Wechselstromwiderstands mit einer Länge (entsprechend dem Scheinwiderstand in Ohm) von 35,18 und einem Winkel im Uhrzeigersinn (also entgegen dem positiven Drehsinn) von 64,77°.
Addition komplexer Widerstände R, L und C
Das obige Beispiel könnte eine Variation dadurch erfahren, dass die Kapazität durch eine Induktivität von 200mH ersetzt wird. Was ergibt sich, wenn das Beispiel mit einer Frequenz von 30kHz durchgerechnet wird?
Die Zeiger der Blindwiderstände von Kapazität und Induktivität zeigen in entgegengesetzte Richtungen. Die Stromrechnung für private Stromabnehmer erstreckt sich nur auf die dem Netz entnommene Wirkleistung. Gewerbliche Verbraucher zahlen für Wirk- und Blindleistung = Scheinleistung. In jedem Fall wäre es eine gute Idee, die Belastung des Stromnetzes durch Blindleistung zu minimieren. Die kann durch eine Kombination von wahlweise Induktivitäten zum Ausgleich von kapazitiver Blindleistung oder durch Kapazitäten zum Ausgleich von induktiver Blindleistung.
In einer Reihenschaltung aus ohmschem Widerstand, Spule und Kapazität fallen an allen 3 Bauteilen Spannungen ab. Durch alle 3 Bauteile fließt der gleiche Strom. Die durch die Induktivität und den Kondensator verursachten (blinden) Spannungen sollen sich gerade kompensieren. Das tun sie, sobald XL und XC einander entsprechen, denn es gilt:
In diesem Fall wird der Scheinwiderstand zum Wirkwiderstand Z = R
XL = XC lässt sich dadurch erreichen, dass:
- die Frequenz variiert wird,
- die Induktivität angepasst wird oder
- die Kapazität angepasst wird.
Bestimmung der Resonanzfrequenz im Reihenschwingkreis
Aus den Scheinwiderständen lässt sich eine Kreisfrequenz ermitteln, bei der der Scheinwiderstand der Induktivität der Schwinwiderstand der Kapazität entspricht. Aus der Kreisfrequenz lässt sich die Resonanzfrequenz ermitteln.
Aus der Kreisfrequenz lässt sich die Resonanzfrequenz ermitteln.
Treffen Wechselgrößen gleicher Frequenz in einem Knoten aufeinander, addieren sie sich zu einer neuen Wechselgröße unter Beibehalt der Frequenz.
Kompensation von Blindleistung durch Kombination von Kondensator und Spule.
Quellen und weiterführende Seiten:
„Elektrotechnik für Ingenieurstudenten nichtelektrotechnischer Fachrichtungen“ Teil 2 Wechselspannungstechnik von Günther Schmitz.
„Wechselstrom und Zeigerdiagramme“ von Wolfgang Bengfort.
Die deutschsprachige Wikipedia mit den Seiten:



